In case you missed it, Oracle Database 26ai was announced last week at Oracle AI World, with a heap of new AI features and capabilities like hybrid vector search, MCP server support, acceleration with NVIDIA and much more – check the link for details.

Of course, I wanted to check it out, and I was thinking about what to do first. I remembered this LinkedIn post from Anders Swanson about implementing custom vector distance functions in Oracle using the new JavaScript capabilities, and I thought that could be something interesting to do, so I am going to show you how to implement and use Jaccard distance for dense vector embeddings for similarity searches.

Now, this is a slightly contrived example, because I am more interested in showing you how to add a custom metric than in the actual metric itself. I chose Jaccard because the actual implementation is pretty compact.

Now, Oracle does already include Jaccard distance, but only for the BINARY data type, which is where Jaccard is mostly used. But there is a version that can be used for continuous/real-valued vectors as well (this version is for dense vectors), and that is what we will implement.

This is the formula for Jaccard similarity for continuous vectors. This is also known as the Tanimoto coefficient. It is the intersection divided by the union (or zero if the union is zero):

To get the Jaccard distance, we just subtract the Jaccard similarity from one.

Before we start, let’s look at a two-dimensional example to get a feel for how it works. Of course, the real vectors created by embedding models have many more dimensions, but it is hard for us to visualize more than two or three dimensions without also introducing techniques like dimensionality reduction and projection).

Here we have two vectors A [5 8] and B [7 4]:

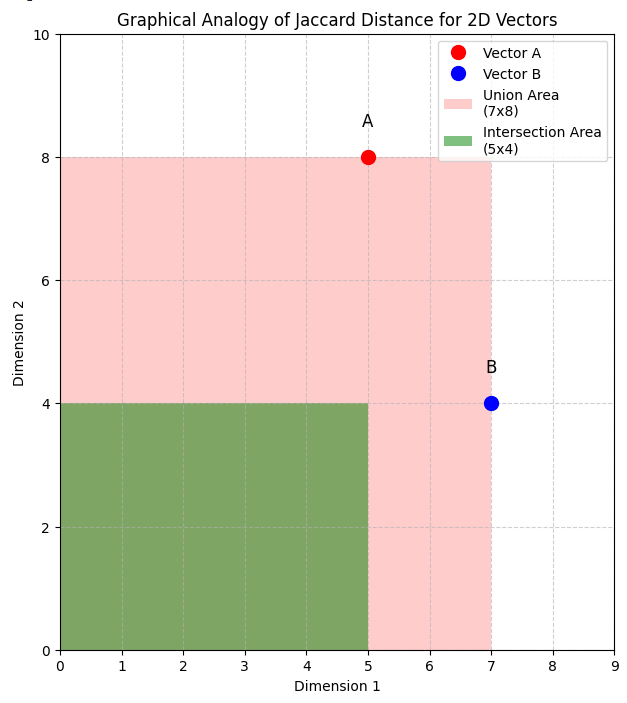
The union is calculated using the max values, as you see in the formular above, so in this example it is 7×8, as shown by the area shaded pink. The intersection is calculated with the min values, so it is 5×4, as shown by the green area.

So in this example, the Jaccard similarity is (7×8) / (5×4) = 56 / 20 = 0.6

And so the Jaccard distance is 1 – 0.6 = 0.4

Ok, now that we have some intuition about how this distance metric works, let’s implement it in Oracle.

Start up an Oracle Database

First, let’s fire up Oracle Database Free 26ai in a container:

docker run -d --name db26ai \
    -p 1521:1521 \
    -e ORACLE_PWD=Welcome12345 \
    -v db26ai-volume:/opt/oracle/oradata \
    container-registry.oracle.com/database/free:latest

This will pull the latest image, which at the time of writing is 26ai (version tag 23.26.0.0). You can check the logs to see when startup is complete, you’ll see a message “DATABASE IS READY TO USE”:

docker logs -f db26ai

Let’s create a user called vector with the necessary privileges:

docker exec -i db26ai sqlplus sys/Welcome12345@localhost:1521/FREEPDB1 as sysdba <<EOF
alter session set container=FREEPDB1;
create user vector identified by vector;
grant connect, resource, unlimited tablespace, create credential, create procedure, create mle, create any index to vector;
commit;
EOF

Now you can connect with your favorite client. I am going to use Oracle SQL Developer for VS Code. See the link for install instructions.

Implement the custom distance function

Open up an SQL Worksheet, or run this in your tool of choice:

create or replace function jaccard_distance("a" vector, "b" vector)
return binary_double 
deterministic parallel_enable
as mle language javascript pure {{
    // check the vectors are the same length
    if (a.length !== b.length) {
        throw new Error('Vectors must have same length');
    }

    let intersection = 0;
    let union = 0;

    for (let i = 0; i < a.length; i++) { 
        intersection += Math.min(a[i], b[i]);
        union += Math.max(a[i], b[i]);
    }

    // handle the case where union is zero (all-zero vectors)
    if (union === 0) {
        return 0;
    }

    const similarity = intersection / union;
    return 1 - similarity;

}};
/

Let’s walk throught this. First, you see that we are creating a function called jaccard_distance which accepts two vectors (a and b) as input and returns a binary_double. This function sugnature is required for distance functions. Next we must include the deterministric keyword and we have also included the parallel_enable keyword so that this function could be used with HNSW vector indexes. For the purposes of this example, you can just ignore those or assume that they are just needed as part of the function signature.

Next you see that we mention this will be an MLE function written in JavaScript, and we added the pure keyword to let the database know that this is a pure function – meaning it has no side effects, it will not update any data, and its output will always be the same for a given set of inputs (i.e., that it is memoizable).

Then we have the actual implementation of the function. First, we check that the vectors have the same length (i.e., the same number of dimensions) which is required for this calculation to be applicable.

Then we work through the vectors and collect the minimums and maximums to calculate the intersection and the union.

Next, we check if the union is zero, and if so we return zero to handle that special case. And finally, we calculate the similarity, then subtract it from one to get the distance and return that.

Using our custom distance function

Great, so let’s test our function. We can start by creating a table t1 to store some vectors:

create table t1 (
    id number,
    v vector(2, float32)
);

And let’s add a couple of vectors, including the one we saw in the example above [5 8]:

insert into t1 (id, v) values 
(1, vector('[5, 8]')),
(2, vector('[1, 2]'));

You can so a simple select statement to see the contents of the table:

select * from t1;

This will give these results:

ID     V
1      [5.0E+000,8.0E+000]
2      [1.0E+000,2.0E+000]

Now let’s use our function to see the Jaccard distance for each vector in our table t1 from the other vector we used in the example above [7 4]:

select 
    v,
    jaccard_distance(v, vector('[7, 4]')) distance
from t1
order by distance; 

This returns these results:

V                       DISTANCE
[5.0E+000,8.0E+000]     0.4
[1.0E+000,2.0E+000]     0.7272727272727273

As you can see, the Jaccard distance from [5 8] to [7 4] is 0.4, as we calculated in the example above, and [1 2] to [7 4] is 0.72…

Let’s see how it works with large embeddings

Ok, two dimension vectors are good for simple visualization, but let’s try this out with some ‘real’ vectors.

I am using Visual Studio Code with the Python and Jupyter extensions from Microsoft installed

Create a new Jupyter Notebook using File > New File… then choose Jupyter Notebook as the type of file, and save your new file at jaccard.ipynb.

First, we need to set up the Python runtime environment. Click on the Select Kernel button (its on the top right). Select Python Environment then Create Python Environment. Select the option to create a Venv (Virtual Environment) and choose your Python interpreter. I recommend using at least Python 3.11. This will download all the necessary files and will take a minute or two.

Now, let’s install the libraries we will need – enter this into a cell and run it:

%pip install oracledb sentence-transformers

Now, connect to the same Oracle database (again, enter this into a cell and run it):

import oracledb

username = "vector"
password = "vector"
dsn = "localhost:1521/FREEPDB1"

try:
    connection = oracledb.connect(
        user=username, 
        password=password, 
        dsn=dsn)
    print("Connection successful!")
except Exception as e:
    print("Connection failed!")

Let’s create a table to hold 1024 dimension vectors that we will create with the mxbai-embed-large-v1 embedding model. Back in your SQL Worksheet, run this statement:

create table t2 (
    id number,
    v vector(1024, float32)
);

Ok, now let’s create some embeddings. Back in your notebook, create a new cell with this code:

import oracledb
from sentence_transformers import SentenceTransformer

# Initialize the embedding model
print("Loading embedding model...")
model = SentenceTransformer('mixedbread-ai/mxbai-embed-large-v1')

# Your text data
texts = [
    "The quick brown fox jumps over the lazy dog",
    "Machine learning is a subset of artificial intelligence",
    "Oracle Database 23ai supports vector embeddings",
    "Python is a popular programming language",
    "Embeddings capture semantic meaning of text"
]

# Generate embeddings
print("Generating embeddings...")
embeddings = model.encode(texts)

Let’s discuss what we are doing in this code. First, we are going to download the embedding model usign the SentenceTransformer. Then, we define a few simple texts that we can use for this example and use the embedding model to create the vector embeddings for those texts.

If you want to see what the embeddings look like, just enter “embeddings” in a cell and run it. In the output you can see the shape is 5 (rows) with 1024 dimensions and the type is float32.

Now, let’s insert the embeddings into our new table t2:

import array 
cursor = connection.cursor()

# Insert data
for i in range(len(embeddings)):
    cursor.execute("""
        INSERT INTO t2 (id, v)
        VALUES (:1, :2)
    """, [i, array.array('f', embeddings[i].tolist())])

connection.commit()
print(f"Successfully inserted {len(texts)} records")

You can take a look at the vectors using the simple query (back in your SQL Worksheet):

select * from t2

Which will show you something like this:

And, now let’s try our distance function with these vectors. Back in your notebook, run this cell. I’ve included the built-in cosine distance as well, just for comparison purposes:

query = array.array('f', model.encode("Antarctica is the driest continent").tolist())

cursor = connection.cursor()
cursor.execute("""
    select 
        id,
        jaccard_distance(v, :1),
        vector_distance(v, :2, cosine)
    from t2
    order by id
""", [query, query])

for row in cursor:
    print(f"id: {row[0]} has jaccard distance: {row[1]} and cosine distance: {row[2]}")

cursor.close()

Your output will look something like this:

id: 0 has jaccard distance: 2.0163214889484307 and cosine distance: 0.7859490566650003
id: 1 has jaccard distance: 2.0118706751976925 and cosine distance: 0.6952327173906239
id: 2 has jaccard distance: 2.0152858933816775 and cosine distance: 0.717824211314015
id: 3 has jaccard distance: 2.0216149035530537 and cosine distance: 0.6455277387099003
id: 4 has jaccard distance: 2.0132575761281766 and cosine distance: 0.6962028121886988

Well, there you go! We implemented and used a custom vector distance function. Enjoy!